Optimization design: Must you trade off between two things you want?

A common trope with presenting solutions to a complicated problem is the tradeoff: you can have this at the expense of that (and vice versa), or of three desirables, you can have only two (the negative of the third is what you'll get.

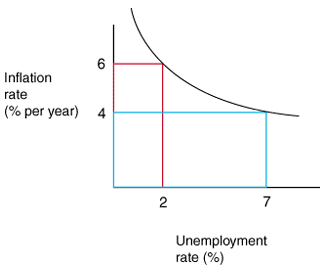
For example, you can have low inflation or low unemployment, but since one can cause increase in the other (if everybody is employed, most people will have more expendable income and so prices will rise to take advantage), you can't have both at the same time.

(the Philip's curve, from SparkNotes)

Many algorithmic problems show solutions with this feature, which is usually the tradeoff between runtime and memory. If you have very little extra room (little available data manipulation space) you might have to make many passed over the data than if you could just have another full copy of the data.  One strategy is to build a big table (often in linear time) in comparison to an algorithm that uses only a couple registers and taking a long time to compute.

Or for a given technology, you want three things: quick production, low cost, and high quality, but any two of these means the third will be bad (see the CAP 'theorem' in distributed database design), you supposedly can only have two of the following, the third being prevented.

• Consistency (all nodes see the same data at the same time)
• Availability (a guarantee that every request receives a response about whether it succeeded or failed)
• Partition tolerance (the system continues to operate despite arbitrary partitioning due to network failures)

(from CAP theorem-Why does it matter)

Supposedly in distributed systems you an only have two of these, because any two denies the third, where a single database on a single machine guarantees all three (the same as the ACID properties).

As rules of thumb, these are all interesting and useful observations to be made about a system. It gives you constraints so that that you shouldn't feel you have to worry about overcoming them.

But this is where design and cleverness come in. The space-time tradeoff or the pick any two of three restriction is just another hurdle to overcome. To solve a problem from the start, you used cleverness to solve it. But it has some drawbacks. In trying to remove the drawbacks, you introduce another drawback, and so you think there is an intimate relationship between the two drawbacks. 

Don't stop there! Your next step of cleverness is to overcome both at the same time, and, as problems go, unless you can prove otherwise, there's no reason you can't make both good at the same time.

For example, take computing Fibonacci's number. F(n) = F(n-1) + F(n-2), F(1) = F(2) = 1.

The first answer is to use recursion and simply compute F(n--1) and F(n-2) directly. That has the drawback that, if left to do it all automatically in the recursion, F(n-k) is repeatedly computed many times. 

(from UCR CS 141 course notes)

Notice there's lots of repeats. 

Instead you can be clever and, once you notice how you compute it by hand, starting from F(3), using the known values F(1) and F(2).Then compute F(4) because you can now that you have F(3) and F(2) and similarly F(5) and so on till you reach F(n). That is linear time but takes linear space:

(from Archimedes Lab)

So we're stuck right, with a tradeoff between time and space, the faster the algorithm the more memory it will use?

Of course not. With all these 'rules', they are just patterns that may or may not follow. It's not necessary that there's a constraint.

For Fibonacci, another observation cuts through both. Instead of going from F(1) to F(n), computing every single item, you really only ever use 2 values at a time (the two previous ones). You don't need to maintain the entire previously computed values in the list. By judicious swapping (using a single temp variable), you can run through the entire table quickly without having to save the whole table, ratcheting upwards quickly.

And for two-out-of-three, there's the example of car manufacturing. Making a car by hand in the late 1800's early 1900's was a painstaking slow process, high cost, and questionable quality. But the assembly line process made all three better: produced cars much faster, much cheaper, and quality much better because every car was made the same way.

Note that with design there's also possibly a tradeoff with simplicity: the more constraints a design tries to handle, the less simple it tends to be. But as with the assembly line method, a simple design, all three are made better. There's no guarantee that more constraints means more complex.

Sure, sometimes the constraints are intertwined, one push must mean another gets pulled. But with appropriate design there may be away around it.