Confidence in association rules is identical to conditional probability

There's something that has bothered me for a while. In presentations of association rule learning (as a method of an unstructured learning method/data mining), the basic principles are:

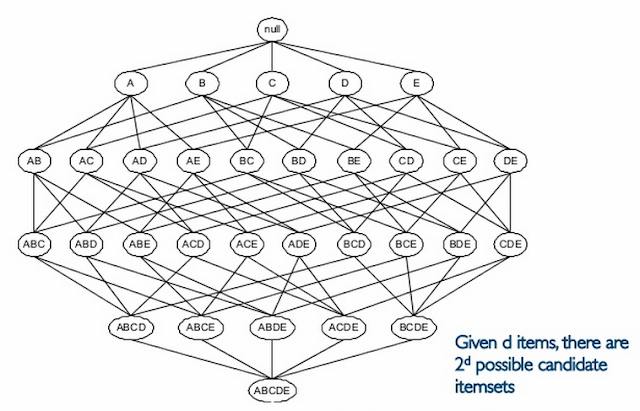
• the store - the set of all possible items {milk, bread, eggs, beer, diapers} = d
• transactions - a list of subsets from all possible items (a transactoin = 1 market basket) eg {milk, bread, eggs, beer}, could be represented by a 0-1 vector of length d. # of transactions = n <= 2^d
• itemsets - a  subset of items in a transaction eg {milk, bread, eggs} or {bread, beer}, k-itemset has k items. 
• support - support count = frequency of occurrence of n item set \sigma({bread}) = 2, support = proportion of an itemset to total transactions s({bread}) = \sigma({bread})/n = 1
• frequent itemset - itemset with s >= given threshold
• association rule: X-> Y,X,Y itemsets, The intention is that X implies Y, or if X appears in a transaction, Y is likely to appear also.
• support (X->Y) = \sigma(X \cup Y), fraction of transactions including both X and Y
• confidence - c(X->Y) = \sigma(X\cup Y)/\sigma(X), how often Y appears in transactions that have X

And the various algorithms (brute force, apriori, Eclat, FP-growth) work on the list of transactions to discover association rules with high confidence. Confidence is the primary concept to be optimized

So what is the difficulty? That last definition of confidence. all that buildup with all that new vocabulary, all so straightforward and sensible, but all so new. There's something about ... confidence... that seems so familiar, but the notation... of implies and support .. it's just...

Of course this has been done elsewhere already.

Confidence is simply the conditional probability of Y given X. That's it. In notation:

Pr(Y | X) = Pr( Y and X) / Pr( X )

which is the probability of Y occurring when restricted to when X is already known to have occurred (not temporally). What might be misleading here is 'and' versus 'union'. In the confidence formula we want the frequency of the itemset and in Pr we want the proportion of  events. There is a just a little step of manipulating subsets and events here; the elements of the set unioned with those of Y is equivlanet to the event of those elements conjoined (= anded) with those of Y. A subset of elements S of T is the dual of the events T a subset of S.

Just a little rejiggering of notation and a whole set of concepts opens up to help think about the space of association rules.

(from Pier Luca Lanzi, DMTM 2015 - 05 Association Rules)